کنترل کننده PID
کنترل کننده PID
در بسیاری از فرآیندهای صنعتی از کنترل کننده تناسبی P یا تناسبی مشتق گیر ،PDتناسبیانتگرال گیر PI و یا کنترل کننده تناسبی– مشتق گیر– انتگرال گیر ،PIDبه عنوان ساختاراصلی کنترل کننده استفاده می شود. هدف از استفاده از حلقه فیدبک و کنترل کننده را می توان بصورت زیر خلاصه کرد:
-
پایداری داخلی
-
دنباله روی از فرمان ورودی ((tracking
-
تضعیف اغتشاش
-
کاهش نویز
-
عدم حساسیت به تغییرات فرآیند
جالب است که تقریبا در کلیه فرآیندهای صنعتی ساختار ساده کنترل کننده PID تمامنیازهای فوق را برآورده می سازد. حتی در برخی از موارد کنترل کننده PI نیز کافی است. درحالت کلی می توان بیان کرد که کنترل کننده PI برای فرآیندهایی که برای سیستمهایی که بامدل درجه یک تقریب زده می شوند، کافی است. در برخی موارد کنترل کننده PID کافی نمی باشد. این موارد را می توان به صورت زیر خلاصه نمود :
-
فرآیندهای با دینامیک رتبه بالاتر از دو
-
سیستمهای با تأخیر زیاد
-
سیستمهای دارای صفر ناپایدار یا سیستمهای غیر مینیمم فاز
-
حذف فرکانسهای خاص در خروجی (فیلتر ناچ (Notch filter
در این مقاله ساختار یک کنترل کننده PID و اثر هر یک از پارامترهای آن بر پاسخ خروجی بررسی می شود. فرآیند کنترل شده مطابق مدار حلقه بسته زیر را در نظر بگیرید:
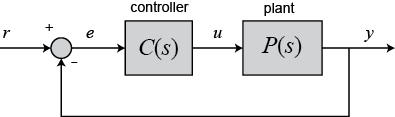
خروجی کنترل کننده PID بصورت زیر می باشد:
متغییر e که نشان دهنده خطای ردیابی است، تفاوت میان مقدار خواسته شده (r) و مقدار واقعی خروجی(y) می باشد.سیگنال خطا وارد کنترل کننده می شود و مقدار مشتق و انتگرال آن محاسبه می شود و سپس سیگنال کنترلی u با ضریبی از سیگنال خطا (kp)،ضریبی از انتگرال خطا (ki)و ضریبی از مشتق خطا (kd) محاسبه می شود. کنترل کننده PID از جمع سه ترم تشکیل شده است:
- ترم تناسبی : Pکه فرمان کنترل متناسب با میزان خطا و با بهره kpتقویت می شود.
- ترم مشتق گیر : Dکه فرمان کنترل متناسب با نرخ تغییرات خطا و با بهره kdتقویت می شود.
- ترم انتگرال گیر : Iفرمان کنترل متناسب با انتگرال این تابع و با بهره kiتقویت می شود.
تابع انتقال کنترل کننده PID بصورت زیر می باشد:
در نرم افزار Matlab تابع انتقال کنترل کننده را می توان بصورت مستقیم تعریف کرد:
Kp = 1;
Ki = 1;
Kd = 1;
s = tf('s');
C = Kp + Ki/s + Kd*s
همچنین می توان از دستورpid نیز استفاده کرد:
C = pid(Kp,Ki,Kd)
حال اجازه دهید تاثیر هریک از این پارامترها را بر پاسخ سیستم توضیح دهیم. بهره تناسبی (kp) باعث کاهش زمان rise time شده ولی خطای دائم را از بین نمی برد. بهره انتگرال گیر (ki) خطای دائم را به ازای ورودی پله از بین می برد ولی باعث کند شدن پاسخ سیستم می شود. بهره مشتق گیر (kd) باعث کم شدن overshoot ، افزایش پایداری و همچنین سریعتر شدن پاسخ سیستم می شود. تاثیر هریک از پارامترهای کنترل کننده را بصورت خلاصه در جدول زیر می توان مشاهده کرد:
|
CL RESPONSE |
RISE TIME |
OVERSHOOT |
SETTLING TIME |
S-S ERROR |
|
Kp |
Decrease |
Increase |
Small Change |
Decrease |
|
Ki |
Decrease |
Increase |
Increase |
Eliminate |
|
Kd |
Small Change |
Decrease | Decrease |
No Change |
مثال: فرض کنید تابع انتقالی بصورت زیر داشته باشیم:
با دستور زیر پاسخ حلقه باز سیستم را به ورودی پله رسم می کنیم:
s = tf('s');
P = 1/(s^2 + 10*s + 20);
step(P)
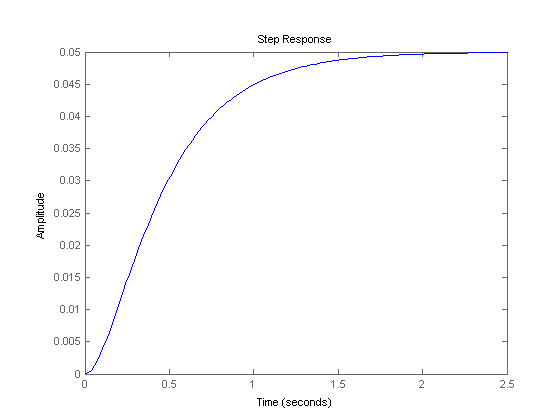
همان طور که مشخص است، خطای حالت دائم 0.95 و همچنین سیستم بسیار کند است.
کنترل کننده تناسبی:
همان طور که جدول بالا نشان می دهد، ترم تناسبی باعث کاهش rise time، افزایش overshoot و کاهش خطای حالت دائم می شود.تابع انتقال حلقه بسته سیستم بالا با ترم تناسبی بصورت زیر است:
با قرار دادن ترم تناسبی برابر 300 با دستور زیر پاسخ حلقه بسته سیستم را به ورودی پله رسم می کنیم:
Kp = 300; C = pid(Kp) T = feedback(C*P,1) t = 0:0.01:2; step(T,t)
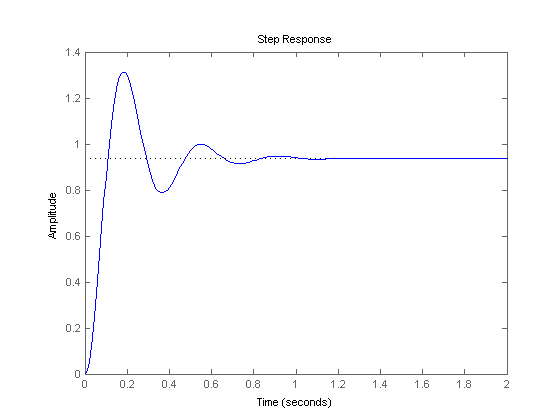
همان طور که شکل بالا نشان می دهد، ترم تناسبی باعث کاهش rise time، افزایش overshoot و کاهش خطای حالت دائم شده است.
کنترل کننده تناسبی- مشتق گیر:
حال بیایید نگاهی به کنترل کننده PD بیاندازیم.همان طور که دیدیم ترم مشتق گیر باعث کاهش overshoot و همچنین settling time می شود. تابع انتقال حلقه بسته سیستم بالا با ترم PD بصورت زیر است:
با قرار دادن ترم تناسبی برابر 300 و ترم مشتق گیر برابر 10 با دستور زیر پاسخ حلقه بسته سیستم را به ورودی پله رسم می کنیم:
Kp = 300; Kd = 10; C = pid(Kp,0,Kd) T = feedback(C*P,1) t = 0:0.01:2; step(T,t)
همان طور که مشخص است ترم مشتق گیر باعث کاهش overshoot و همچنین settling time شده است و همچنین تاثیر کمی بر rise time و خطای حالت دائم داشته است.
کنترل کننده تناسبی-انتگرال گیر- مشتق گیر:
تابع انتقال حلقه بسته سیستم بالا با ترم PID بصورت زیر است:
بعد از چند بار سعی و خطا مقادیر زیر برای پاسخ مناسب در نظر گرفته شد:
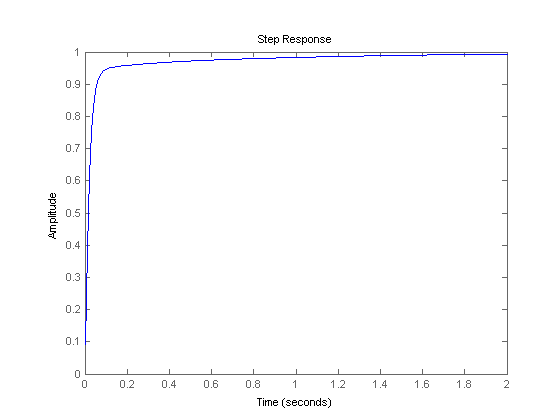
Kp = 350; Ki = 300; Kd = 50; C = pid(Kp,Ki,Kd) T = feedback(C*P,1); t = 0:0.01:2; step(T,t)
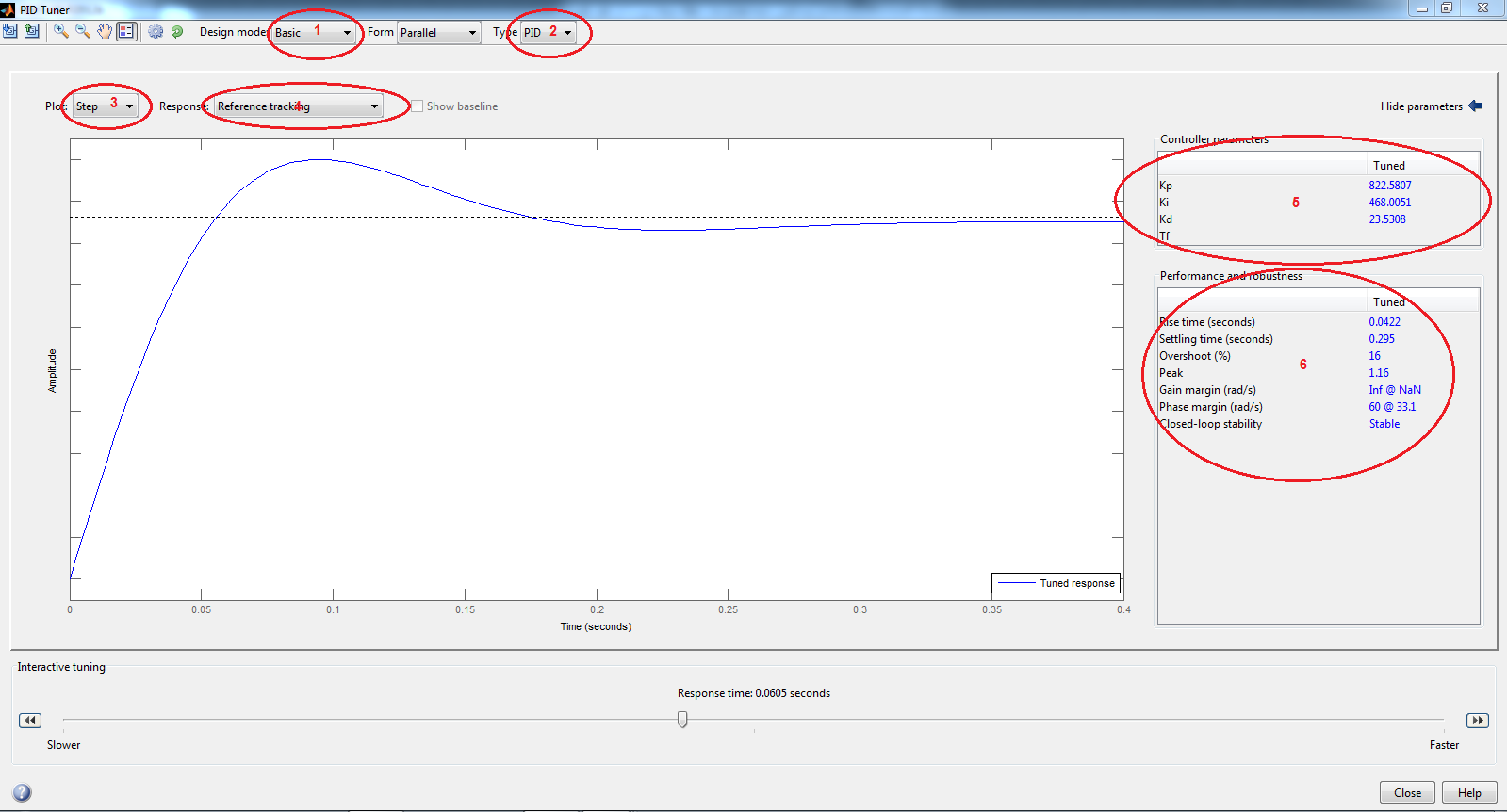
همان طور که مشخص است پاسخ هیچ overshoot و خطای حالت دائمی ندارد و همچنین دارای rise time سریعی می باشد. نرم افزار Matlab دارای ابزاری بنام pidtool می باشد که خیلی راحت می توان یک کنترل کننده PID را بصورت گرافیکی تنظیم کرد.با دستور زیر که پارامتر اول آن تابع انتقال سیستم و پارامتر دوم نوع کنترل کننده را مشخص می کند،می توان وارد محیط PID Tuner شد:
pidtool(P,C)
1)در این قسمت نوع طراحی مشخص می شود(براساس زمان پاسخ یا بر اساس پهنای باند و…)
2)در این قسمت نوع کنترل کننده مشخص می شود.
3)در این قسمت نمایش پاسخ در محدوده زمان یا در محدوده فرکانس(Bode) مشخص می شود.
4)در این قسمت منحنی انتخاب می شود.
5)در این قسمت مقادیر پارامترهای کنترل کننده مشخص می شود.
6)در این قسمت مشخصات پاسخ دیده می شود.(مقدار overshoot،rise time و…)
- ۰ نظر
- ۰۱ اسفند ۹۶ ، ۲۳:۰۴

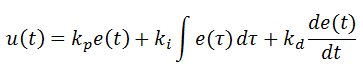
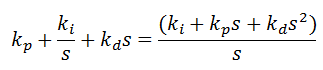
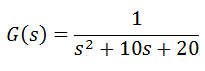
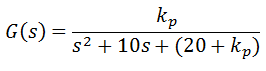
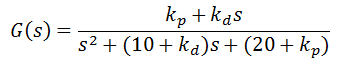

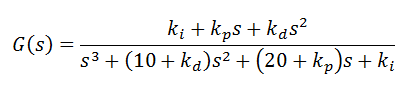


 مثال ااز سه حلقه تو در توی for در متلب:
مثال ااز سه حلقه تو در توی for در متلب:
Setting Up OpenCV on Windows with Eclipse, MinGW and Cmake